We are attempting to find the muzzle velocity of a potato as it leaves a pneumatically powered "spud gun." There are three basic parts in one of these guns: A pressure chamber, a valve, and a barrel. The basic idea is: We build up a large amount of pressure in the pressure chamber which, when the valve is opened, will propel the potato down the barrel.

For simplification purposes, we will consider the valve as a "black box" apparatus, that instantaneously opens when triggered, so its affects can be ignored for these calculations. We are additionally considering both the pressure chamber and barrel to be of equal radius, to cut down on air friction. For the pressure chamber, consider a PVC pipe of radius r, and length L0. The barrel will also have a radius r, but will have a length Lb.

The pressure on the inside of the chamber initially, right when the valve is first closed, is equal to the outside atmospheric pressure – roughly 1atm. The number of moles of air inside at this point is calculated using the following equation:

(1)

where p is the atmospheric pressure, V is the volume of the pressure chamber, R is the ideal gas law constant, and T is temperature.

As the chamber is pressurized, more moles of air are being forced into the chamber. The number of added moles is calculated once again using equation (1). The sum of these n's is the total number of moles of air inside the pressurized chamber. The total pressure on the inside, even after the valve has been opened can be found by a solving equation (1) for pressure, and substituting the total number of moles for n

(3)

(4)

For our case:

(5)

Substituting n from equation (1) yields:

(6)

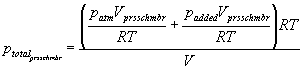
Simplifying:

(7)

The volume variables in the numerator and in the denominator do not cancel. Since, when the valve is opened, the potato moves down the barrel the volume of the pressure "chamber" changes. Thus, as the total volume increases the amount of pressure decreases. However, the volume of a cylinder is:

(8)

where A is the cross-sectional surface area of the cylinder and L is its length. (And since the surface area is the same at all lengths of the pipe, A will cancel.) Thus, substituting equation (8) for V in equation (7) produces an expression where the internal pressure is a function of the "current" length of the pressure chamber, determined by adding the length the potato moved to the initial length of the pressure chamber:

(9)

However, we need to find the force that this pressure exerts on the potato. The relationship between force and pressure is defined as:

(10)

So, substituting equation (9) in equation (10) gives us the force that the potato feels from the air in the pressure chamber as a function of its distance along the barrel:

(11)

But this is only one of the relevant forces acting on the potato. There is still pressure from the atmosphere pushing the potato back down the barrel. Since the barrel is open, we will make a simplifying assumption that, ignoring the compression of air in the barrel and the potato shoots out, this pressure will be constant at any length of the barrel. Thus, the force exerted by atmospheric pressure on the potato is:

(12)

Friction also opposes the motion of the potato. We were unable to find a good way to theoretically model this friction, so we measured it experimentally (see whole lengthy non-overly-technical write-up page). Additionally, the magnitude of the force of friction usually does not depend on velocity (, where μ is the coefficient of kinetic friction, and N is the force normal to the plane of motion), so it too is constant at any point along the barrel. For now, we will simply identify the force of friction by a label under the variable F.

So, the total sum of the forces acting on the potato, at any length along the barrel is:

(13)

And explicitly:

(14)

But we still need to find the muzzle velocity. The potato undergoes a change in kinetic energy. The work that the air does on the potato on its trip down the barrel is the change in kinetic energy of the potato. If we can find work, we can find the change in kinetic energy. Since work is generally defined as:

(15)

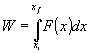
We can substitute equation (14) for force:

(16)

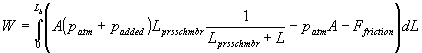
with our origin set at the valve, and the length of the barrel as L_b. Simplifying the integral gives:

(17)

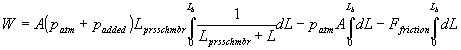
After evaluation the integral we get:

(18)

Simplifying:

(19)

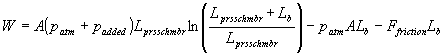
Since this work equals the change in kinetic energy:

(20)

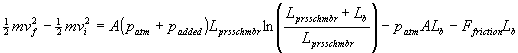
Since the initial velocity is 0:

(21)

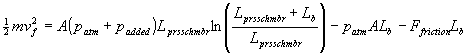
Solving for v gives a final expression for the muzzle velocity of the potato:

(22)

Equation (22) is the most general equation for the muzzle velocity for any lengths pressure chamber and barrel. However, in any real case, the total length of the gun is the sum of the barrel and pressure chamber lengths. Explicitly:

(23)

This length is our first "real" number – i.e. the person designing the gun has decided he only wants the gun to be 1.5m, for example. Thus, we can get the muzzle velocity to be dependant only on one "unknown" variable – the length of the pressure chamber, for example – which allows an easy setup for maximizing the muzzle velocity. So, substituting equation (23) for the barrel length into equation (22) gives us the muzzle velocity as a "function" of the pressure chamber length:

(24)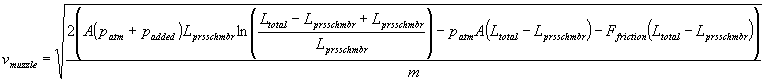Simplifying:

(25)

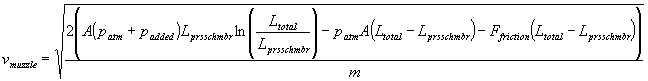
A plot with arbitrary values for A, L_total, p_atm, p_added, m and F_friction looks like this:

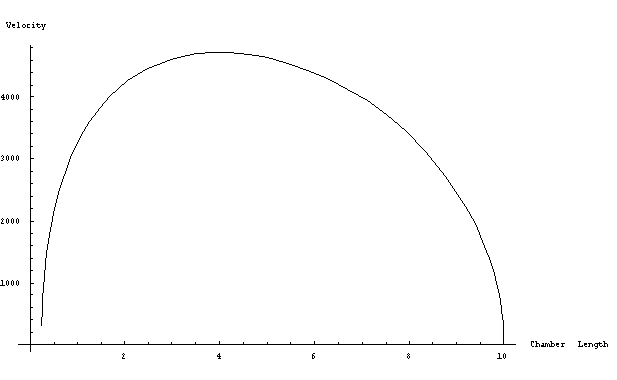
This plot is rather neat. When the pressure chamber length is too small, force of the starting pressure is not enough to overcome the combined forces of friction and atmospheric pressure, yielding no plot. At around .25, there is enough volume in the pressure chamber to produce some, but comparatively little velocity. When the chamber length is around 4 there is a clear maximum, which drops off gradually as the barrel length decreases, not allowing enough time for acceleration of the potato. Fortunately for our purposes, there is a rather gentle slope around the maximum, which means that technically, if our measurements are a bit off, the decrease in ultimate muzzle velocity will not be that drastic.

So, by taking the derivative of equation (25), plugging in actual experimental numbers for friction, internal surface area of the pipe, etc, and solving for when the derivative is zero, we can find the chamber length that creates the highest muzzle velocity. And then we can solve equation (23) for barrel length, and viola! we have a highly efficient and powerful spud gun.